Портал о строительстве и ремонтных работах

Реологические свойства материалов (упругость, пластичность и вязкость) описывают характером зависимости напряжения от деформации. Под деформацией понимается изменение формы и (или) объема тела без нарушения его сплошности. Течение — про­цесс непрерывного роста деформации во времени без увеличения нагрузки. Деформации бывают обратимыми (исчезающими после снятия нагрузки) и необратимыми (остаточными или пластиче­скими).

Обратимыми являются упругие и эластические деформации. Их природа различна. Упругие деформации обусловлены изменением расстояния между атомами, а эластические — изменением кон­формации макромолекул полимеров (см. подразд. 14.4). Остаточ­ные деформации в кристаллических телах возникают в результате скольжения дислокаций за счет последовательного перескока ато­мов со своего места на соседнее. Это приводит к необратимому смещению одних частей кристалла по отношению к другим час­тям.

Любую деформацию, независимо от того, происходит она при растяжении, сжатии, изгибе или кручении, можно разложить на две составляющие: изменение объема и изменение формы. При всестороннем равномерном сжатии или растяжении все материа­лы ведут себя одинаково — как упругие тела. Следовательно, по характеру деформации объема тела неразличимы. Изменение же формы в зависимости от нагрузки определяется тремя фундамен­тальными свойствами, присущими всем без исключения матери­алам: упругостью, пластичностью и вязкостью.

Каждое из этих свойств в отдельности описывают законом по­ведения некоторого идеального тела, эквивалентом которого мо­жет служить механическая модель.

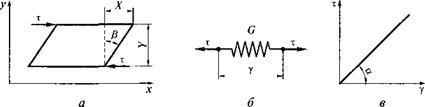
Деформация формоизменения — это деформация сдвига у, кото­рая равна отношению смещения двух точек элемента вдоль оси х к расстоянию между ними по оси у: у = X/ Y= tg (3 (рис. 2.9, а).

Закон упругости Гука. Закон упругости Гука — это закон пря­мой пропорциональности между напряжением и деформацией, характерный для идеально упругого тела, моделью которого явля­ется спиральная пружина (рис. 2.9, б, в): % = Gy; G= tga, где G — модуль упругости при сдвиге, равный тангенсу угла наклона гра­фика зависимости т = /(у). Модуль упругости зависит только от свойств данного материала и является одной из его характерис­тик.

Закон пластичности Сен-Венана —Кулона. Деформация идеаль­но пластичного тела отсутствует (у = 0) при напряжениях сдвига меньше предела текучести (т < тт). При достижении предела теку­чести (т = тт) возникает течение материала с той или иной скоро­стью у ft, где / — время. Скорость деформации у/ / реальных тел при т = const зависит от их вязкости. Моделью идеально пластич-

б

ного тела является элемент трения (рис. 2.10, а). Пока сила, сдви­гающая предмет, не превысит силу трения тт, движения не про­исходит (рис. 2.10, б). Предел текучести является характеристикой пластичности материала.

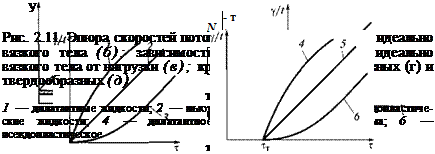
Закон вязкости Ньютона. Представим жидкость, находящуюся в зазоре толщиной Yмежду двумя пластинами равной площади А (рис. 2.11, а). Пусть верхняя пластина под действием силы Fдви­жется в направлении оси х со скоростью и. В результате трения пластина увлекает за собой жидкость, которая течет ламинарно (послойно), причем слои жидкости движутся с разной скоростью и(у), зависящей от координаты у. Между слоями действуют силы трения, которые тем больше, чем сильнее различаются скорости слоев. Это различие скоростей характеризуют отношением и/ Y.

Согласно закону Ньютона в случае идеальной (ньютоновской) жидкости напряжение трения между слоями (или равное ему на­пряжение сдвига т — F/А) прямо пропорционально и/ Y т = ги/ Y. Поскольку и — X/t, то: и/ Y — Х/t/ Y= у/Г. Таким образом, напря­жение сдвига прямо пропорционально скорости сдвиговой дефор­мации: т = цу/t.

Коэффициент пропорциональности г называется динамиче­ским коэффициентом, вязкости. Он зависит только от свойств жид­кости и ее температуры. Из закона Ньютона следует, что едини­цей измерения т| в системе СИ является паскаль-секунда (Па • с). В системе СГС за единицу вязкости принят пуаз (П) (1 Па • с = = 10 П). Вязкость воды при 20,5 °С равна 1 сП (1 сП = 0,01 П). Для воздуха р = 0,02 сП.

Деформация ньютоновской жидкости при т = const прямо про­порциональна времени и не ограничена во времени: у = (x/p)t.

Величина, обратная вязкости (1/р), в случае жидкостей назы­вается текучестью, а в случае высококонцентрированных коагу­ляционных структур — подвижностью.

Моделью идеально вязкого тела является устройство, состо­ящее из цилиндра с вязкой жидкостью и поршня с отверстия­ми в днище (рис. 2.1 1, б). При перемещении поршня жидкость перетекает через отверстия из одной части цилиндра в другую. Чем меньше вязкость жидкости, тем быстрее она перетекает и тем быстрее движется поршень при данном усилии. График за-

г д

висимости скорости деформации от приложенного напряжения (рис. 2.11, в) представляет собой прямую линию, котангенс угла наклона которой равен коэффициенту вязкости: т| = ctga; при этом т| = const.

Реологические свойства реальных структур. Постоянство ц ха­рактерно только для идеальных (ньютоновских) жидкостей. Для реальных веществ т| зависит от напряжения или скорости сдвига (рис. 2.11, г, д). Среди строительных материалов большинство ко­агуляционных структур характеризуются кривой 6. Специфическим свойством таких структур является тиксотропия — способность структуры после разрушения в результате перемешивания само­произвольно восстанавливаться. Например, цементное тесто при перемешивании уменьшает свою вязкость (разжижается), а остав­ленное в покое тесто возвращается в исходное состояние. Способ­ность коагуляционных структур к самовосстановлению позволяет перемешивать, укладывать и уплотнять строительные смеси без потери конечной прочности материалов.

Моделирование реологических свойств реальных тел можно про­изводить с помощью различных сочетаний рассмотренных иде­альных моделей. При последовательном соединении элементов (G— V—N) общее напряжение модели равно напряжению в каждом из них: т = тс = tv = xN, а деформация и скорость деформации модели складываются из соответствующих значений для элемен­тов: Y = Yc + lv + In’, у/t = (у/ t)G+ (у/1) v + (у/1) N. При параллельном соединении элементов (С|| К||Д/) Т = Тс + Тк+ Т№ У = Ус = Ук= Удг,

у/1 = (у/t)G = (у /t)v= (y/t)N.

Комментарии закрыты.