Портал о строительстве и ремонтных работах

Прочность — это способность материала сопротивляться разру­шению под действием внешних сил или других факторов, вызы­вающих внутренние напряжения в материале.

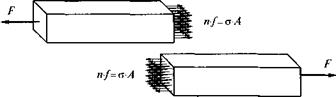
Если растягивать стержень силой F, то его длина увеличится. Следовательно, увеличатся расстояния между атомами и возрас­тут силы их взаимного притяжения. Эти внутренние силы уравно­вешивают внешнюю силу F. Условие равновесия составляют с по­мощью метода сечений. Разрежем мысленно стержень на две час­ти и рассмотрим одну из них (рис. 2.3). Чтобы равновесие этой части не изменилось, действие отброшенной части нужно заме­нить большим числом внутренних сил/, приложенных к каждому атому. Если в поперечном сечении п атомов, то условие равнове­сия примет вид: fn = F.

Принято относить внутренние силы не к каждому атому, а к единице площади поперечного сечения и называть эту величину напряжением: <5=fn/A = F/А, где А — площадь поперечного сече­ния стержня.

Единицей измерения напряжения в системе СИ является пас­каль (Па): 1 Па = 1 Н/м2. Эта единица слишком мелкая для стро­ительных материалов, поэтому обычно используют мегапаскаль (МПа): 1 МПа= 106 Па. Иногда используется единица технической системы — кгс/см2 (кгс — килограмм силы). 1 МПа = 9,81 кгс/см2.

Рис. 2.3. Иллюстрация метода сечений (условие равновесия отсеченной части)

Поскольку п/А = const, то о = const/, а значит, напряжения зависят только от вида данных атомов, т. е. от свойств вещества.

Увеличивая далее силу F, можно развести атомы на такие рас­стояния, на которых они потеряют связь между собой. Произой­дет разрыв образца. К моменту разрушения напряжение достигнет своего максимального значения, принимаемого за предел проч­ности образца R.

При экспериментальном определении предела прочности при растяжении /?р образец измеряют в поперечном сечении, затем растягивают в разрывной машине до разрыва и регистрируют мак­симальную нагрузку при испытании Fm. AX. Предел прочности опре­деляют по формуле

ЛР = (2.2)

где А0 — первоначальная площадь поперечного сечения, измерен­ная до испытания.

В действительности площадь поперечного сечения не постоян­на — она уменьшается с увеличением длины стержня, и истин­ный предел прочности при растяжении всегда немного больше предела прочности, рассчитанного по формуле (2.2).

Значения прочности материалов, получаемые эксперименталь­но, оказываются примерно на два порядка ниже теоретических значений, вычисленных из предположения, что предел прочнос­ти, так же как напряжение, пропорционален силе взаимодействия атомов/ На самом деле это верно только для идеальных кристал­лов; для реальных тел прочность определяется наличием дефек­тов (см. подразд. 1.2).

Так, теоретическая прочность стекла на растяжение составляет около 104 МПа. Микротрещины и неоднородности, неизбежные при изготовлении стекла, снижают его прочность примерно в 100 раз. В результате появления на поверхности стекла дополни­тельных дефектов (микротрещин, царапин) при резке, упаковке, транспортировании и монтаже фактическая прочность при растя­жении уменьшается еще в 2 — 3 раза и составляет 30…60 МПа.

Согласно статистической теории прочности, пионерами кото­рой являются шведский ученый В. Вейбул и российские ученые Т. А. Конторова и Я. И. Френкель, прочность образца лимитирова­на наиболее опасным дефектом, содержащимся в его объеме. С уве­личением объема образца повышается вероятность существова­ния в нем крупного дефекта, поэтому средняя прочность об­разцов одного и того же материала возрастает с уменьшением их размеров. Например, прочность при изгибе образцов окон­ного стекла шириной 100 мм составила 60 МПа, а шириной 200 мм — 45 МПа.

Влияние размеров образцов на прочность называется масштаб­ным фактором. Чтобы исключить влияние масштабного фактора на прочность, установлены стандартные размеры образцов для каждого материала. В некоторых случаях пользуются масштабными коэффициентами, равными отношению прочности образцов про­извольных размеров к прочности стандартных образцов.

Распределение дефектов в образцах является случайным, по­этому прочность одного образца не может служить характеристи­кой материала. Требуется испытать значительное число одинако­вых образцов, чтобы достоверно охарактеризовать прочность ма­териала.

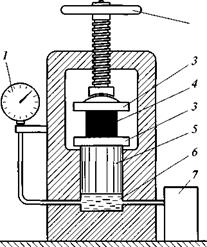
Испытание на сжатие. Его выполняют на образцах, как прави­ло, кубической или цилиндрической формы с помощью гидрав­лического пресса (рис. 2.4). Образец 4 зажимают между плитами пресса 3, вращая маховик 2. Включают электродвигатель масляно­го насоса 7 и по отклонению стрелки манометра 1 наблюдают за повышением давления масла р в цилиндре 6 пресса. При этом на поршень 5 и соответственно на образец 4 действует сжимающая сила F= рАп, где Ап — площадь поршня. Нагружение образца про­должают до начала его разрушения, которое определяется по об­ратному движению стрелки манометра после максимального от­клонения. Измерительные системы современных гидравлических прессов, как правило, показывают непосредственно значение силы F, действующей на образец.

Предел прочности при осевом сжатии равен отношению мак­симальной нагрузки Fmax = рттАп к первоначальной площади по­перечного сечения образца: Л<.ж = F^JA^.

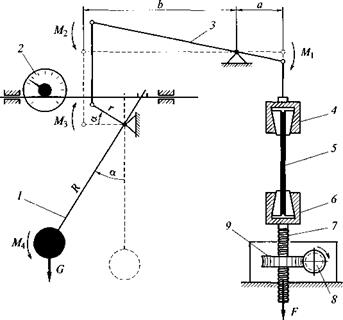
Испытание на растяжение. Его выполняют на разрывных маши­нах с гидравлической или механической системой нагружения. В ме­ханической системе выигрыш в силе получают с помощью рыча­гов или винтового устройства с редуктором. В этом случае машины оборудуют чаще всего маятниковым силоизмерителем (рис. 2.5). Растягивающая сила F, приложенная к образцу 5 через нижний захват 6, создается за счет перемещения вниз винта 7, который

Рис. 2.4. Схема гидравлического пресса:

1 — манометр; 2 — маховик подъема плиты; 3 — опорные плиты; 4 — образец; 5 —
поршень; 6 — цилиндр; 7 — масляный насос

Рис. 2.5. Схема маятникового силоизмерителя разрывной машины:

1 — маятник; 2 — индикатор силы; 3 — рычаг; 4— верхний захват; 5 — образец;
6 — нижний захват; 7 — винт; 8 — червяк; 9 — шестерня перемещения винта

удерживается от вращения и движется поступательно по внутрен­ней резьбе шестерни 9, приводимой во вращение от электродви­гателя червяком 8. Перемещение вниз верхнего захвата 4 вызывает поворот рычага 3 и отклонение маятника /, связанного со стрел­кой индикатора силы 2, на угол а. Исходя из равенства моментов Мх = М2- Fa и Л/3 = М4= G7?sin а при равновесии можно составить два уравнения, из совместного решения которых следует, что сила Fпрямо пропорциональна тангенсу угла a: F — Alga, где К = = GbR/(ar) — постоянная машины, определяемая соотношением плеч рычага 3 и маятника / и весом G груза маятника.

Предел прочности при осевом растяжении рассчитывают по формуле (2.2).

Соотношение /?р//?сЖ зависит от природы материала и его стро­ения: у древесины, стеклопластиков и других материалов с на­правленным волокнистым армированием Rp > Д. ж; у стали Ар = Д. ж; у каменных материалов, бетона, керамики Rp < Л<.ж.

Испытание на изгиб. Его выполняют по схеме балки, свободно лежащей на двух опорах и нагруженной либо одной (посередине пролета), либо двумя (через 1/3 пролета) сосредоточенными си­лами (рис. 2.6).

Предел прочности при изгибе Аи равен отношению максималь­ного изгибающего момента Мтах к моменту сопротивления попе­речного сечения W: RH = Мтт/ W. Изгибающий момент зависит от схемы нагружения балки. В схеме, представленной на рис. 2.6, а, Мпах = Fmaxl/4; в схеме, представленной на рис. 2.6, б, Мтлх = Етах//6. Момент сопротивления зависит от формы поперечного сечения образца. Для круглого сечения W = тш?3/32; для прямоугольного сечения W = bh2/6, где d — диаметр образца; b — ширина сече­ния; h — высота сечения (размер в направлении разрушающей силы).

Удельная прочность (коэффициент конструктивного качества Ак. к) — отношение предела прочности материала к его плотнос­ти: Ккк = R/уд. При растяжении наиболее высокие значения Rp/yQ,

а б

а — балка, нагруженная одной (посередине пролета) силой; б — балка, нагру-
женная двумя (через 1/3 пролета) сосредоточенными силами

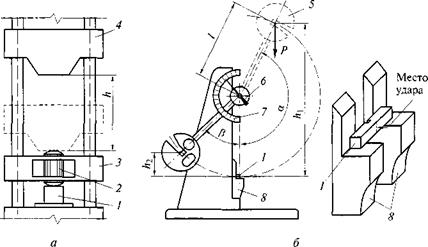
Рис. 2.7. Схемы копра Педжа (а) и маятникового копра (б): І — образец; 2 — боек; 3 — подбабок; 4 — падающий груз (баба); 5 — маятник; 6 — стрелка; 7 — шкала; 8 — опоры

МПа/(кг/м3), имеют стеклопластики — 0,22, древесина — 0,20; у стали Rn/jn = 0,05…0,13. При сжатии у обычного бетона &.ж/уо = = 0,01 …0,02; у кирпича — 0,005…0,015.

Ударная вязкость (прочность при ударе) — способность матери­алов сопротивляться разрушению при ударе. Материалы, легко разрушающиеся при ударе, называются хрупкими. Ударную вяз­кость характеризуют работой, затраченной на разрушение образ­цов при стандартном испытании, отнесенной к единице объема (Дж/м3) или площади поперечного сечения образца (Дж/м2).

Природные каменные материалы испытывают в образцах-ци­линдрах на копре Педжа (рис. 2.7, а), подвергая их ударам падаю­щего груза (бабы) 4. Образец 1 прижимают к наковальне подбаб — ком 3, имеющим подпружиненный боек 2, по которому произво­дятся удары: первый — с высоты 1 см, второй — с высоты 2 см, третий — с высоты 3 см и так далее до разрушения образца.

Ударную вязкость определяют по формуле

а = Р( 1+2 + … +n)/V,

где Р — вес бабы; п — число ударов; V — объем образца.

По числу ударов породы подразделяются на слабые (п < 8), средние (п = 8… 16) и ударопрочные (п > 16).

Сталь, древесину и пластмассы испытывают на маятниковом копре (рис. 2.7, б, в). Маятник 5 поднимают на определенный угол а и фиксируют в этом положении. Образец в виде балочки уста-

навливают на две опоры 8, пролет между которыми можно регу­лировать. Стальные образцы имеют надрез со стороны, противо­положной удару. При падении маятник разрушает образец, затра­чивая часть своей потенциальной энергии, равной Phx, и по инер­ции отклоняется на угол (3, на что расходуется работа Ph2. Величи­на (Phx — Ph2) есть работа, затраченная на разрушение образца. Ударная вязкость определяется по формуле

а = P(hx — hi)/S = /Y(cosa — cos[3)/5,

где P — вес маятника; У — площадь поперечного сечения образ­ца: / — длина маятника.

Значение углов а и (3 определяется показанием стрелки 6, от­клоняемой маятником, по шкале 7.

Твердость — способность материалов сопротивляться царапаю­щему действию или внедрению других тел. Эта способность зави­сит от твердости других тел и оценивается по отношению к ним.

Для минералов принята качественная оценка твердости с по­мощью шкалы Мооса (табл. 2.3), по которой 10 минералов, при­нятых за эталоны, расположены в порядке возрастания твердости так, что каждый последующий минерал оставляет царапину на предыдущем. Твердость остальных минералов «привязывают» к дан­ной шкале, присваивая им тот или иной номер, который, одна­ко, не является количественной характеристикой. Так, алмаз (№ 10) тверже апатита (№ 5) почти в 20 раз, а не в 2 раза, как можно было бы подумать, судя по их номерам на шкале.

Таблица 2.3 Номер минерала по шкале Мооса Минерал Ориентировочная твердость, МПа Предмет, оставляющий царапину на данном минерале 1 Тальк 20 Мягкий карандаш 2 Г ипс 360 Ноготь 3 Кальцит 1 090 Медная монета 4 Флюорит 1 890 Железный гвоздь 5 Апатит 5 360 Острие ножа 6 Ортоклаз 7 950 Стекло 7 Кварц 11 200 Острие напильника 8 Топаз 14 270 Наждачный круг 9 Корунд 20 600 Алмаз К) Алмаз 100600 Не царапается ничем

При количественной оценке твердости в испытуемый матери­ал под определенной нагрузкой вдавливают так называемый ин — дентор (шарик, конус, пирамидку и т. д.). По нагрузке и размерам полученного отпечатка рассчитывают показатель твердости. В за­висимости от формы индентора различают показатель твердости по Бринеллю (шарик), по Виккерсу (квадратная пирамидка), по Кнуппу (пирамидка с ромбовидным основанием), по Роквеллу (алмазный конус).

Твердость по Шору устанавливают в зависимости от высоты отскока стального шарика при падении на поверхность твердого тела.

Результаты испытаний на твердость одного и того же материа­ла различными методами не совпадают, но согласуются между собой.

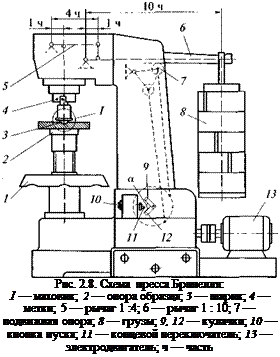Твердость по Бринеллю определяется с помощью пресса Бри — нелля (рис. 2.8). В шлифованную или полированную поверхность образца вдавливают шарик из твердой закаленной стали. В зависи­мости от толщины образца применяют шарик диаметром D, рав­ным 10; 5 или 2,5 мм. При испытании стали нагрузку на шарик в зависимости от ожидаемой твердости берут равной 30Z)2; 10О2 или 2,5D2. Время действия нагрузки составляет 10 с — для черных ме­таллов; 30 или 60 с — для цветных металлов. Число твердости по

Бринеллю (НВ) — это отношение нагрузки F к площади сфери­ческой поверхности Асф отпечатка диаметром d:

НВ= F/ Асф.

Площадь сферической поверхности

_п D(D-jD2-d2)

2

Образец кладут на опору образца 2. Вращая маховик 1, прижи­мают образец к шарику 3 до совмещения меток 4. Кнопкой 10 включают электродвигатель 13, в результате чего кулачки 9 и 12 начинают перемещаться по часовой стрелке. Одновременно опора 7 опускается вниз, освобождая рычаг 6. Нагрузка на шарик пере­дается от груза 8 через систему рычагов 5 и 6 с общим соотноше­нием плеч 1:40. Кулачок 12, дойдя до концевого переключателя 11, изменяет направление вращения электродвигателя 13. При этом кулачки 9 и 12 поворачиваются против часовой стрелки, а опора 7 поднимается вверх, блокируя рычаг 6. Кулачок 9 выключает электродвигатель. Время действия нагрузки регулируют, изменяя угол а между плечами кулачков 9 и 12.

С увеличением твердости материалов повышается их износоус­тойчивость и истираемость, но затрудняется механическая обра­ботка.

Истираемость материала характеризуется потерей массы об­разца с единицы площади истирания, полученной при стандарт­ном испытании на круге истирания с абразивом в виде кварцево­го песка или наждака.

Износостойкость — способность материала сопротивляться из­нашиванию при трении и ударном воздействии в реальных усло­виях.

Комментарии закрыты.