Портал о строительстве и ремонтных работах

Архивы за Сентябрь 2015

3.1. Общие сведения

Древесина — древнейший строительный материал — не утра­тила своего значения и в настоящее время несмотря на ряд суще­ственных недостатков, к которым относятся способность к заг­ниванию, горючесть, анизотропность, а также усушка и разбуха­ние, приводящие к короблению и растрескиванию изделий. Вместе с тем строительная древесина выгодно отличается от других матери­алов высокой прочностью при малой плотности (500…700 кг/м3), легкостью механической обработки. По прочности при сжатии вдоль волокон древесина не уступает бетону, а по прочности при изги­бе значительно превосходит его. При этом древесина легче бетона примерно в 4 раза. По удельной прочности (отношению прочнос­ти к плотности) древесина занимает второе место, уступая толь­ко некоторым стеклопластикам. Пористо-капиллярное строение древесины обусловливает ее низкую теплопроводность, позволя­ющую использовать древесину в качестве стенового материала. Толщина стены из деревянного бруса при одинаковой теплоза­щите помещения в 2,5 — 3 раза меньше толщины кирпичной сте­ны.

По своему химическому составу и взаимодействию с окружаю­щей средой древесина не только безопасна для здоровья челове­ка, но и создает благоприятные условия для его обитания, поэто­му мебель из натуральной древесины и отделка ею помещений ценятся высоко. Как получение (произрастание), так и уничтоже­ние древесины являются естественными процессами и происхо­дят без загрязнения окружающей среды. Использование древеси­ны в качестве строительного материала имеет место на завершаю­щей стадии ее природного цикла — стадии уничтожения, кото­рую невозможно исключить, но можно замедлить. Недолговеч­ность древесины является «платой» за ее экологическую чистоту.

Из многочисленных пород деревьев, произрастающих на тер­ритории России, промышленное значение имеют около полутора
десятков наиболее распространенных из них: из лиственных — дуб, ясень, каштан, вяз, ильм, карагач, бархатное дерево, ди — морфант, лох; из хвойных — сосна, лиственница, кедр, ель, пих­та, тис.

Надлежащее качество строительных материалов и изделий обес­печивается путем выполнения технических требований к их свой­ствам, устанавливаемых Государственными стандартами Россий­ской Федерации (ГОСТ), отраслевыми стандартами (ОСТ) и тех­ническими условиями предприятий (ТУ). Это позволяет устано­

вить единую систему маркировки материалов, условий их изго­товления, хранения и транспортирования. Наличие системы госу­дарственной стандартизации предполагает возможность контроля государственными органами качества продукции предприятий.

Для того чтобы исключить расхождения в оценке свойств мате­риалов, государственной стандартизации подлежат также методы испытаний, которыми руководствуются испытательные лабора­тории.

От долговечности материалов зависит срок службы зданий и сооружений. Долговечность материалов устанавливают на основа­нии опыта эксплуатации конструкций в тех или иных условиях или прогнозируют исходя из результатов лабораторных испыта­ний, моделирующих воздействия внешней среды. Процессы, при­водящие к постепенному разрушению конструкций, зависят от вида материала и условий его эксплуатации. К таким процессам относятся выветривание каменных материалов, коррозия бетона или стали, старение битумов и полимеров, загнивание древесины и др. Все факторы разрушения можно подразделить на физиче­ские (растворяющее и адсорбционное действие воды и органи­ческих жидкостей, температурные воздействия, совместное дей­ствие воды и мороза); химические (воздействие кислорода возду­ха, растворов солей, кислот, щелочей, природных и промышлен­ных газов) и биологические (действие грибов, животных и расти­тельных организмов).

Повышения долговечности сооружений добиваются обычно двумя путями:

1) рациональным устройством конструкции и правильным применением материалов;

2) совершенствованием материалов, в первую очередь, повы­шением различных видов их стойкости: химической, атмосфер­ной, температурной, водостойкости, морозостойкости и др.

Реологические свойства материалов (упругость, пластичность и вязкость) описывают характером зависимости напряжения от деформации. Под деформацией понимается изменение формы и (или) объема тела без нарушения его сплошности. Течение — про­цесс непрерывного роста деформации во времени без увеличения нагрузки. Деформации бывают обратимыми (исчезающими после снятия нагрузки) и необратимыми (остаточными или пластиче­скими).

Обратимыми являются упругие и эластические деформации. Их природа различна. Упругие деформации обусловлены изменением расстояния между атомами, а эластические — изменением кон­формации макромолекул полимеров (см. подразд. 14.4). Остаточ­ные деформации в кристаллических телах возникают в результате скольжения дислокаций за счет последовательного перескока ато­мов со своего места на соседнее. Это приводит к необратимому смещению одних частей кристалла по отношению к другим час­тям.

Любую деформацию, независимо от того, происходит она при растяжении, сжатии, изгибе или кручении, можно разложить на две составляющие: изменение объема и изменение формы. При всестороннем равномерном сжатии или растяжении все материа­лы ведут себя одинаково — как упругие тела. Следовательно, по характеру деформации объема тела неразличимы. Изменение же формы в зависимости от нагрузки определяется тремя фундамен­тальными свойствами, присущими всем без исключения матери­алам: упругостью, пластичностью и вязкостью.

Каждое из этих свойств в отдельности описывают законом по­ведения некоторого идеального тела, эквивалентом которого мо­жет служить механическая модель.

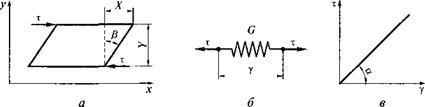
Деформация формоизменения — это деформация сдвига у, кото­рая равна отношению смещения двух точек элемента вдоль оси х к расстоянию между ними по оси у: у = X/ Y= tg (3 (рис. 2.9, а).

Закон упругости Гука. Закон упругости Гука — это закон пря­мой пропорциональности между напряжением и деформацией, характерный для идеально упругого тела, моделью которого явля­ется спиральная пружина (рис. 2.9, б, в): % = Gy; G= tga, где G — модуль упругости при сдвиге, равный тангенсу угла наклона гра­фика зависимости т = /(у). Модуль упругости зависит только от свойств данного материала и является одной из его характерис­тик.

Закон пластичности Сен-Венана —Кулона. Деформация идеаль­но пластичного тела отсутствует (у = 0) при напряжениях сдвига меньше предела текучести (т < тт). При достижении предела теку­чести (т = тт) возникает течение материала с той или иной скоро­стью у ft, где / — время. Скорость деформации у/ / реальных тел при т = const зависит от их вязкости. Моделью идеально пластич-

Рис. 2.9. Деформация сдвига (а), модель идеально упругого тела Гука (6) и зависимость напряжения в теле Гука от деформации сдвига (в)

Рис. 2.10. Модель идеально пластич­ного тела (а) и зависимость дефор­мации этого тела от напряжения (б)	У
Тт ^777777777/ У а
т
Ту

 

б

ного тела является элемент трения (рис. 2.10, а). Пока сила, сдви­гающая предмет, не превысит силу трения тт, движения не про­исходит (рис. 2.10, б). Предел текучести является характеристикой пластичности материала.

Закон вязкости Ньютона. Представим жидкость, находящуюся в зазоре толщиной Yмежду двумя пластинами равной площади А (рис. 2.11, а). Пусть верхняя пластина под действием силы Fдви­жется в направлении оси х со скоростью и. В результате трения пластина увлекает за собой жидкость, которая течет ламинарно (послойно), причем слои жидкости движутся с разной скоростью и(у), зависящей от координаты у. Между слоями действуют силы трения, которые тем больше, чем сильнее различаются скорости слоев. Это различие скоростей характеризуют отношением и/ Y.

Согласно закону Ньютона в случае идеальной (ньютоновской) жидкости напряжение трения между слоями (или равное ему на­пряжение сдвига т — F/А) прямо пропорционально и/ Y т = ги/ Y. Поскольку и — X/t, то: и/ Y — Х/t/ Y= у/Г. Таким образом, напря­жение сдвига прямо пропорционально скорости сдвиговой дефор­мации: т = цу/t.

Коэффициент пропорциональности г называется динамиче­ским коэффициентом, вязкости. Он зависит только от свойств жид­кости и ее температуры. Из закона Ньютона следует, что едини­цей измерения т| в системе СИ является паскаль-секунда (Па • с). В системе СГС за единицу вязкости принят пуаз (П) (1 Па • с = = 10 П). Вязкость воды при 20,5 °С равна 1 сП (1 сП = 0,01 П). Для воздуха р = 0,02 сП.

Деформация ньютоновской жидкости при т = const прямо про­порциональна времени и не ограничена во времени: у = (x/p)t.

Величина, обратная вязкости (1/р), в случае жидкостей назы­вается текучестью, а в случае высококонцентрированных коагу­ляционных структур — подвижностью.

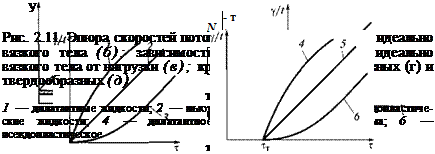
Моделью идеально вязкого тела является устройство, состо­ящее из цилиндра с вязкой жидкостью и поршня с отверстия­ми в днище (рис. 2.1 1, б). При перемещении поршня жидкость перетекает через отверстия из одной части цилиндра в другую. Чем меньше вязкость жидкости, тем быстрее она перетекает и тем быстрее движется поршень при данном усилии. График за-

г д

висимости скорости деформации от приложенного напряжения (рис. 2.11, в) представляет собой прямую линию, котангенс угла наклона которой равен коэффициенту вязкости: т| = ctga; при этом т| = const.

Реологические свойства реальных структур. Постоянство ц ха­рактерно только для идеальных (ньютоновских) жидкостей. Для реальных веществ т| зависит от напряжения или скорости сдвига (рис. 2.11, г, д). Среди строительных материалов большинство ко­агуляционных структур характеризуются кривой 6. Специфическим свойством таких структур является тиксотропия — способность структуры после разрушения в результате перемешивания само­произвольно восстанавливаться. Например, цементное тесто при перемешивании уменьшает свою вязкость (разжижается), а остав­ленное в покое тесто возвращается в исходное состояние. Способ­ность коагуляционных структур к самовосстановлению позволяет перемешивать, укладывать и уплотнять строительные смеси без потери конечной прочности материалов.

Моделирование реологических свойств реальных тел можно про­изводить с помощью различных сочетаний рассмотренных иде­альных моделей. При последовательном соединении элементов (G— V—N) общее напряжение модели равно напряжению в каждом из них: т = тс = tv = xN, а деформация и скорость деформации модели складываются из соответствующих значений для элемен­тов: Y = Yc + lv + In’, у/t = (у/ t)G+ (у/1) v + (у/1) N. При параллельном соединении элементов (С|| К||Д/) Т = Тс + Тк+ Т№ У = Ус = Ук= Удг,

у/1 = (у/t)G = (у /t)v= (y/t)N.

Прочность — это способность материала сопротивляться разру­шению под действием внешних сил или других факторов, вызы­вающих внутренние напряжения в материале.

Если растягивать стержень силой F, то его длина увеличится. Следовательно, увеличатся расстояния между атомами и возрас­тут силы их взаимного притяжения. Эти внутренние силы уравно­вешивают внешнюю силу F. Условие равновесия составляют с по­мощью метода сечений. Разрежем мысленно стержень на две час­ти и рассмотрим одну из них (рис. 2.3). Чтобы равновесие этой части не изменилось, действие отброшенной части нужно заме­нить большим числом внутренних сил/, приложенных к каждому атому. Если в поперечном сечении п атомов, то условие равнове­сия примет вид: fn = F.

Принято относить внутренние силы не к каждому атому, а к единице площади поперечного сечения и называть эту величину напряжением: <5=fn/A = F/А, где А — площадь поперечного сече­ния стержня.

Единицей измерения напряжения в системе СИ является пас­каль (Па): 1 Па = 1 Н/м2. Эта единица слишком мелкая для стро­ительных материалов, поэтому обычно используют мегапаскаль (МПа): 1 МПа= 106 Па. Иногда используется единица технической системы — кгс/см2 (кгс — килограмм силы). 1 МПа = 9,81 кгс/см2.

Рис. 2.3. Иллюстрация метода сечений (условие равновесия отсеченной части)

Поскольку п/А = const, то о = const/, а значит, напряжения зависят только от вида данных атомов, т. е. от свойств вещества.

Увеличивая далее силу F, можно развести атомы на такие рас­стояния, на которых они потеряют связь между собой. Произой­дет разрыв образца. К моменту разрушения напряжение достигнет своего максимального значения, принимаемого за предел проч­ности образца R.

При экспериментальном определении предела прочности при растяжении /?р образец измеряют в поперечном сечении, затем растягивают в разрывной машине до разрыва и регистрируют мак­симальную нагрузку при испытании Fm. AX. Предел прочности опре­деляют по формуле

ЛР = (2.2)

где А0 — первоначальная площадь поперечного сечения, измерен­ная до испытания.

В действительности площадь поперечного сечения не постоян­на — она уменьшается с увеличением длины стержня, и истин­ный предел прочности при растяжении всегда немного больше предела прочности, рассчитанного по формуле (2.2).

Значения прочности материалов, получаемые эксперименталь­но, оказываются примерно на два порядка ниже теоретических значений, вычисленных из предположения, что предел прочнос­ти, так же как напряжение, пропорционален силе взаимодействия атомов/ На самом деле это верно только для идеальных кристал­лов; для реальных тел прочность определяется наличием дефек­тов (см. подразд. 1.2).

Так, теоретическая прочность стекла на растяжение составляет около 104 МПа. Микротрещины и неоднородности, неизбежные при изготовлении стекла, снижают его прочность примерно в 100 раз. В результате появления на поверхности стекла дополни­тельных дефектов (микротрещин, царапин) при резке, упаковке, транспортировании и монтаже фактическая прочность при растя­жении уменьшается еще в 2 — 3 раза и составляет 30…60 МПа.

Согласно статистической теории прочности, пионерами кото­рой являются шведский ученый В. Вейбул и российские ученые Т. А. Конторова и Я. И. Френкель, прочность образца лимитирова­на наиболее опасным дефектом, содержащимся в его объеме. С уве­личением объема образца повышается вероятность существова­ния в нем крупного дефекта, поэтому средняя прочность об­разцов одного и того же материала возрастает с уменьшением их размеров. Например, прочность при изгибе образцов окон­ного стекла шириной 100 мм составила 60 МПа, а шириной 200 мм — 45 МПа.

Влияние размеров образцов на прочность называется масштаб­ным фактором. Чтобы исключить влияние масштабного фактора на прочность, установлены стандартные размеры образцов для каждого материала. В некоторых случаях пользуются масштабными коэффициентами, равными отношению прочности образцов про­извольных размеров к прочности стандартных образцов.

Распределение дефектов в образцах является случайным, по­этому прочность одного образца не может служить характеристи­кой материала. Требуется испытать значительное число одинако­вых образцов, чтобы достоверно охарактеризовать прочность ма­териала.

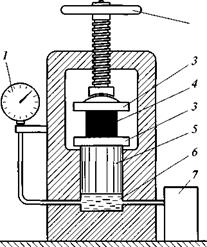
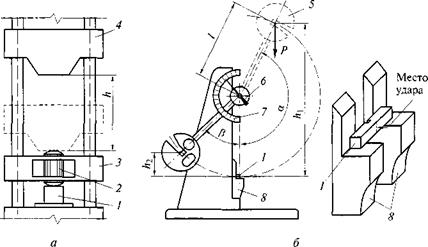
Испытание на сжатие. Его выполняют на образцах, как прави­ло, кубической или цилиндрической формы с помощью гидрав­лического пресса (рис. 2.4). Образец 4 зажимают между плитами пресса 3, вращая маховик 2. Включают электродвигатель масляно­го насоса 7 и по отклонению стрелки манометра 1 наблюдают за повышением давления масла р в цилиндре 6 пресса. При этом на поршень 5 и соответственно на образец 4 действует сжимающая сила F= рАп, где Ап — площадь поршня. Нагружение образца про­должают до начала его разрушения, которое определяется по об­ратному движению стрелки манометра после максимального от­клонения. Измерительные системы современных гидравлических прессов, как правило, показывают непосредственно значение силы F, действующей на образец.

Предел прочности при осевом сжатии равен отношению мак­симальной нагрузки Fmax = рттАп к первоначальной площади по­перечного сечения образца: Л<.ж = F^JA^.

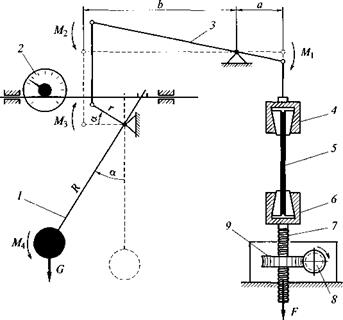
Испытание на растяжение. Его выполняют на разрывных маши­нах с гидравлической или механической системой нагружения. В ме­ханической системе выигрыш в силе получают с помощью рыча­гов или винтового устройства с редуктором. В этом случае машины оборудуют чаще всего маятниковым силоизмерителем (рис. 2.5). Растягивающая сила F, приложенная к образцу 5 через нижний захват 6, создается за счет перемещения вниз винта 7, который

Рис. 2.4. Схема гидравлического пресса:

1 — манометр; 2 — маховик подъема плиты; 3 — опорные плиты; 4 — образец; 5 —
поршень; 6 — цилиндр; 7 — масляный насос

Рис. 2.5. Схема маятникового силоизмерителя разрывной машины:

1 — маятник; 2 — индикатор силы; 3 — рычаг; 4— верхний захват; 5 — образец;
6 — нижний захват; 7 — винт; 8 — червяк; 9 — шестерня перемещения винта

удерживается от вращения и движется поступательно по внутрен­ней резьбе шестерни 9, приводимой во вращение от электродви­гателя червяком 8. Перемещение вниз верхнего захвата 4 вызывает поворот рычага 3 и отклонение маятника /, связанного со стрел­кой индикатора силы 2, на угол а. Исходя из равенства моментов Мх = М2- Fa и Л/3 = М4= G7?sin а при равновесии можно составить два уравнения, из совместного решения которых следует, что сила Fпрямо пропорциональна тангенсу угла a: F — Alga, где К = = GbR/(ar) — постоянная машины, определяемая соотношением плеч рычага 3 и маятника / и весом G груза маятника.

Предел прочности при осевом растяжении рассчитывают по формуле (2.2).

Соотношение /?р//?сЖ зависит от природы материала и его стро­ения: у древесины, стеклопластиков и других материалов с на­правленным волокнистым армированием Rp > Д. ж; у стали Ар = Д. ж; у каменных материалов, бетона, керамики Rp < Л<.ж.

Испытание на изгиб. Его выполняют по схеме балки, свободно лежащей на двух опорах и нагруженной либо одной (посередине пролета), либо двумя (через 1/3 пролета) сосредоточенными си­лами (рис. 2.6).

Предел прочности при изгибе Аи равен отношению максималь­ного изгибающего момента Мтах к моменту сопротивления попе­речного сечения W: RH = Мтт/ W. Изгибающий момент зависит от схемы нагружения балки. В схеме, представленной на рис. 2.6, а, Мпах = Fmaxl/4; в схеме, представленной на рис. 2.6, б, Мтлх = Етах//6. Момент сопротивления зависит от формы поперечного сечения образца. Для круглого сечения W = тш?3/32; для прямоугольного сечения W = bh2/6, где d — диаметр образца; b — ширина сече­ния; h — высота сечения (размер в направлении разрушающей силы).

Удельная прочность (коэффициент конструктивного качества Ак. к) — отношение предела прочности материала к его плотнос­ти: Ккк = R/уд. При растяжении наиболее высокие значения Rp/yQ,

а б

а — балка, нагруженная одной (посередине пролета) силой; б — балка, нагру-
женная двумя (через 1/3 пролета) сосредоточенными силами

Рис. 2.7. Схемы копра Педжа (а) и маятникового копра (б): І — образец; 2 — боек; 3 — подбабок; 4 — падающий груз (баба); 5 — маятник; 6 — стрелка; 7 — шкала; 8 — опоры

МПа/(кг/м3), имеют стеклопластики — 0,22, древесина — 0,20; у стали Rn/jn = 0,05…0,13. При сжатии у обычного бетона &.ж/уо = = 0,01 …0,02; у кирпича — 0,005…0,015.

Ударная вязкость (прочность при ударе) — способность матери­алов сопротивляться разрушению при ударе. Материалы, легко разрушающиеся при ударе, называются хрупкими. Ударную вяз­кость характеризуют работой, затраченной на разрушение образ­цов при стандартном испытании, отнесенной к единице объема (Дж/м3) или площади поперечного сечения образца (Дж/м2).

Природные каменные материалы испытывают в образцах-ци­линдрах на копре Педжа (рис. 2.7, а), подвергая их ударам падаю­щего груза (бабы) 4. Образец 1 прижимают к наковальне подбаб — ком 3, имеющим подпружиненный боек 2, по которому произво­дятся удары: первый — с высоты 1 см, второй — с высоты 2 см, третий — с высоты 3 см и так далее до разрушения образца.

Ударную вязкость определяют по формуле

а = Р( 1+2 + … +n)/V,

где Р — вес бабы; п — число ударов; V — объем образца.

По числу ударов породы подразделяются на слабые (п < 8), средние (п = 8… 16) и ударопрочные (п > 16).

Сталь, древесину и пластмассы испытывают на маятниковом копре (рис. 2.7, б, в). Маятник 5 поднимают на определенный угол а и фиксируют в этом положении. Образец в виде балочки уста-

навливают на две опоры 8, пролет между которыми можно регу­лировать. Стальные образцы имеют надрез со стороны, противо­положной удару. При падении маятник разрушает образец, затра­чивая часть своей потенциальной энергии, равной Phx, и по инер­ции отклоняется на угол (3, на что расходуется работа Ph2. Величи­на (Phx — Ph2) есть работа, затраченная на разрушение образца. Ударная вязкость определяется по формуле

а = P(hx — hi)/S = /Y(cosa — cos[3)/5,

где P — вес маятника; У — площадь поперечного сечения образ­ца: / — длина маятника.

Значение углов а и (3 определяется показанием стрелки 6, от­клоняемой маятником, по шкале 7.

Твердость — способность материалов сопротивляться царапаю­щему действию или внедрению других тел. Эта способность зави­сит от твердости других тел и оценивается по отношению к ним.

Для минералов принята качественная оценка твердости с по­мощью шкалы Мооса (табл. 2.3), по которой 10 минералов, при­нятых за эталоны, расположены в порядке возрастания твердости так, что каждый последующий минерал оставляет царапину на предыдущем. Твердость остальных минералов «привязывают» к дан­ной шкале, присваивая им тот или иной номер, который, одна­ко, не является количественной характеристикой. Так, алмаз (№ 10) тверже апатита (№ 5) почти в 20 раз, а не в 2 раза, как можно было бы подумать, судя по их номерам на шкале.

Таблица 2.3 Номер минерала по шкале Мооса Минерал Ориентировочная твердость, МПа Предмет, оставляющий царапину на данном минерале 1 Тальк 20 Мягкий карандаш 2 Г ипс 360 Ноготь 3 Кальцит 1 090 Медная монета 4 Флюорит 1 890 Железный гвоздь 5 Апатит 5 360 Острие ножа 6 Ортоклаз 7 950 Стекло 7 Кварц 11 200 Острие напильника 8 Топаз 14 270 Наждачный круг 9 Корунд 20 600 Алмаз К) Алмаз 100600 Не царапается ничем

При количественной оценке твердости в испытуемый матери­ал под определенной нагрузкой вдавливают так называемый ин — дентор (шарик, конус, пирамидку и т. д.). По нагрузке и размерам полученного отпечатка рассчитывают показатель твердости. В за­висимости от формы индентора различают показатель твердости по Бринеллю (шарик), по Виккерсу (квадратная пирамидка), по Кнуппу (пирамидка с ромбовидным основанием), по Роквеллу (алмазный конус).

Твердость по Шору устанавливают в зависимости от высоты отскока стального шарика при падении на поверхность твердого тела.

Результаты испытаний на твердость одного и того же материа­ла различными методами не совпадают, но согласуются между собой.

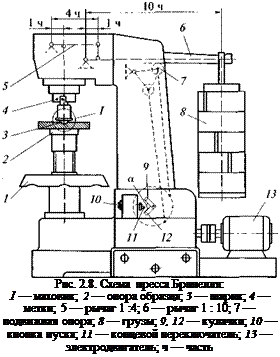Твердость по Бринеллю определяется с помощью пресса Бри — нелля (рис. 2.8). В шлифованную или полированную поверхность образца вдавливают шарик из твердой закаленной стали. В зависи­мости от толщины образца применяют шарик диаметром D, рав­ным 10; 5 или 2,5 мм. При испытании стали нагрузку на шарик в зависимости от ожидаемой твердости берут равной 30Z)2; 10О2 или 2,5D2. Время действия нагрузки составляет 10 с — для черных ме­таллов; 30 или 60 с — для цветных металлов. Число твердости по

Бринеллю (НВ) — это отношение нагрузки F к площади сфери­ческой поверхности Асф отпечатка диаметром d:

НВ= F/ Асф.

Площадь сферической поверхности

_п D(D-jD2-d2)

2

Образец кладут на опору образца 2. Вращая маховик 1, прижи­мают образец к шарику 3 до совмещения меток 4. Кнопкой 10 включают электродвигатель 13, в результате чего кулачки 9 и 12 начинают перемещаться по часовой стрелке. Одновременно опора 7 опускается вниз, освобождая рычаг 6. Нагрузка на шарик пере­дается от груза 8 через систему рычагов 5 и 6 с общим соотноше­нием плеч 1:40. Кулачок 12, дойдя до концевого переключателя 11, изменяет направление вращения электродвигателя 13. При этом кулачки 9 и 12 поворачиваются против часовой стрелки, а опора 7 поднимается вверх, блокируя рычаг 6. Кулачок 9 выключает электродвигатель. Время действия нагрузки регулируют, изменяя угол а между плечами кулачков 9 и 12.

С увеличением твердости материалов повышается их износоус­тойчивость и истираемость, но затрудняется механическая обра­ботка.

Истираемость материала характеризуется потерей массы об­разца с единицы площади истирания, полученной при стандарт­ном испытании на круге истирания с абразивом в виде кварцево­го песка или наждака.

Износостойкость — способность материала сопротивляться из­нашиванию при трении и ударном воздействии в реальных усло­виях.

Теплофизические свойства материалов необходимы при про­ектировании ограждающих конструкций зданий и сооружений и определяют выбор материалов для них. Проблему термонапряжен­ного состояния конструкций также невозможно решить без зна­ния этих свойств.

Теплоемкость. Если сообщить телу количество теплоты Q, то тем­пература его повысится на At градусов. Отношение С = Q/At назы­вается теплоемкостью системы. Характеристикой материала явля­ется удельная теплоемкость с, представляющая собой количество теплоты (Дж), которое нужно сообщить телу массой 1 кг, чтобы его температура поднялась на 1 К: с — С/т, где т — масса тела.

Приближенный результат для многофазных систем можно по­лучить по правилу аддитивности, если для каждой из п фаз извест­ны удельная теплоемкость с, и масса т,:

Теплопроводность. Теплопроводность — это способность тела передавать теплоту внутри себя от горячих частей к холодным.

Если нагревать на огне один конец металлического стержня, то очень скоро можно почувствовать, что и другой его конец ста­новится горячим. Это происходит потому, что атомы на горячем конце, увеличив частоту и амплитуду своих колебаний, воздей­ствуют на соседние, менее нагретые атомы, заставляя их коле­баться сильнее. Те, в свою очередь, передают энергию колебаний дальше — так теплота распространяется от горячего конца стерж­ня к холодному. Теплота во всех твердых телах передается колеба­ниями решетки (атомных ядер). В металлах в переносе теплоты участвуют также электроны проводимости, причем их вклад в теп­лопроводность на два порядка выше, чем решетки. Поэтому теп­лопроводность металлов очень высокая.

В основе классической теории теплопроводности лежит закон Фурье, который для плоскопараллельной однородной стенки (рис. 2.2) с температурой, изменяющейся только по толщине стенки 8 и не зависящей от времени т, имеет вид

Q = XU] h)Sx, (2.1)

8

где Q — количество теплоты, прошедшее через стенку толщиной 8, площадью S за время т при разности температур на поверхностях стены 0 = (/, -12); А — коэффициент пропорциональности, называ­емый коэффициентом внутренней теплопроводности, Вт/(м-°С).

Из уравнения (2.1) следует, что коэффициент А = Q8/(OSx) — это количество теплоты, проходящей через однородную стенку толщиной 1 м, площадью 1 м2 за время 1 с при разности темпера­тур на поверхностях стены 1 К.

Закон Фурье не учитывает зависимость А от температуры. Для плохо проводящих материалов при температуре t = -100…800°С эта зависимость может быть описана уравнением X, = А0(1 + Р0, где А„ Х0 —

нию Xt = Ao(l + 0,0032/), где XQ = 0,0238 Вт/(м — °С). Другие факто­ры, влияющие на X, относятся к особенностям материала, поэто­му X является характеристикой его теплоизоляционных свойств. Чем ниже X, тем лучше теплоизоляционные свойства материала. Эти свойства зависят главным образом от его пористости и влаж­ности.

При заполнении объема материала порами (воздухом) его теп­лопроводность резко снижается, так как X неподвижного воздуха очень мал. Конвекция (перемещение) воздуха в порах повышает теплопроводность. Для уменьшения конвекции размеры пор дол­жны быть как можно меньше. Лучшими теплоизоляционными материалами являются материалы с высокой (близкой к 100%) пористостью и очень малыми изолированными друг от друга по­рами. Теплопроводность таких материалов приближается к тепло­проводности воздуха.

Плотность связана с истинной пористостью линейной зависи­мостью у0 = р(1 — П„/100), поэтому служит косвенной характери­стикой теплопроводности. Чем меньше у0, тем меньше X и тем лучше теплоизоляционные свойства, но ниже прочность матери­ала.

Влага, попавшая в поры, сильно повышает теплопроводность материалов. Коэффициент X сухого воздуха (без конвективного теплообмена) составляет 0,024, а для воды X = 0,8 Вт/(м — °С), что

Таблица 2.2 Материал Теплофизические характеристики Коэффициент теплопроводности X, Вт/(м • °С) Удельная теплоемкость с, кДж/(кг • °С) КЛТР, 10-ус Гранит 2,9 0,84 1,0…1,5 Бетон (тяжелый) 1,4 1,05 1,0… 1,4 Кирпич (кладка) 0,8 0,80 — Сосна(поперек волокон) 0,17 2,7 0,4…0,7 Пенополистирол 0,045 1,7 6…9 Воздух (непод­вижный) 0,024 — — Вода 0,58 4,18 — Лед 2,3 2,1 — Сталь 58 0,46 1,1…1,2 Медь 401 — —

в 25 раз больше. При замене воздуха в порах материала водой теп­лопроводность растет почти линейно с увеличением объемной влажности WQ:

Xw = X + 51V0,

где X — теплопроводность сухого материала; 8 — угловой коэффи­циент, определяемый экспериментально (обычно 8 находится в пределах 0,002…0,004).

В случае замерзания воды в порах теплопроводность увеличится почти в 4 раза, так как X льда составляет 2,32 Вт/(м • °С). Следова­тельно, необходимо защищать теплоизоляционные материалы от увлажнения.

Отношение толщины слоя материала 8 к коэффициенту тепло­проводности X называется сопротивлением теплопередаче: R-b/X.

Тепловое расширение материалов. Тепловое расширение мате­риалов характеризуется коэффициентом линейного температурно­го расширения (КЛТР), который показывает, на какую долю уве­личивается длина изделия при нагревании на 1 °С. Значения КЛТР и других теплофизических характеристик для некоторых материа­лов приведены в табл. 2.2.

Влажность W (%) — это содержание влаги в материале в дан­ных условиях: W — [{mw-т)/т] 100, где т„ — масса материала во влажном состоянии; т — масса высушенного материала.

С увеличением влажности возрастает объем (набухание), сни­жается прочность и увеличивается теплопроводность материалов.

Гигроскопичность — это способность материала адсорбиро­вать парообразную влагу из воздуха. Вследствие гигроскопично­сти высушенные материалы, находясь на воздухе, приобретают некоторую влажность, которая называется равновесной, так как она изменяется с влажностью воздуха, стремясь к равновесию с ней. Наиболее гигроскопичным материалом является древе­сина; ее влажность в воздушно-сухом состоянии может состав­лять 9… 15 %.

Водостойкость — это способность материала противостоять растворяющему, адсорбционному и химическому воздействию воды. Водостойкость характеризуют коэффициентом размягчения кр, равным отношению прочности материала, насыщенного во­дой, к прочности сухого материала: кр = Лнас/Rcyx.

Коэффициент размягчения изменяется от 0 (глина) до 1 (сталь). Материалы с кр < 0,8 являются неводостойкими, их не применя­ют в конструкциях, работающих в воде.

Водонепроницаемость характеризуют наибольшим перепадом давления воды, который выдерживает материал в условиях стан­дартного испытания (см. подразд. 9.5).

Понятие морозостойкость неоднозначно для абсолютно плот­ных и пористых материалов. Для материалов на основе битумов и полимеров, а также для металлов под морозостойкостью понима­ют способность сохранять пластические свойства на морозе и ха­рактеризуют морозостойкость наинизшей температурой, при ко­торой материал еще не становится хрупким и его можно дефор­мировать, не опасаясь образования трещин.

Морозостойкость бетона, кирпича и других пористых материа­лов — это способность насыщенных водой образцов сохранять свою прочность при многократном замораживании и оттаивании воды в порах. Морозное разрушение материала происходит в результате
расширения воды при переходе в лед (при одинаковой массе объем льда больше объема воды примерно на 9 %).

Морозостойкость характеризуется маркой (F15, F25, ,

F1000) — числом циклов замораживания и оттаивания, которое выдерживает материал в условиях стандартного испытания. Мар­ку по морозостойкости задают в проекте сооружения в зависимо­сти от возможного насыщения водой и прогнозируемого числа переходов температуры через 0 °С.

Прямой метод оценки морозостойкости включает в себя:

1) подготовку двух серий образцов (основных и контрольных);

2) предварительное насыщение образцов водой;

3) выполнение заданного маркой числа циклов заморажива­ния (в морозильной камере при t < -17 °С) и оттаивания (в воде при t > 17 °С) основных образцов;

4) испытание образцов обеих серий на прочность при сжатии.

Отношение прочности основных образцов к прочности кон­трольных называется коэффициентом морозостойкости (XMp3 = = Лосн/ЛКОнтр)- Считается, что материал выдержал заданное число циклов, если коэффициент морозостойкости оказался не ниже некоторого нормированного значения (для кирпича — 0,75; для гидротехнического бетона — 0,95).

Морозостойкость тем выше, чем меньшую долю составляет от­крытая пористость; больше в порах остается защемленного возду­ха, который легко сжимается при расширении замерзающей воды и не дает подняться давлению; выше прочность материала при растяжении.

Плотность у„ (кг/м3) — это масса единицы объема материала в естественном состоянии:

Ъ — т / ^ест>

где т — масса высушенного образца; Vecr — объем образца в естественном состоянии.

Материал	Структурные характеристики
Абсолютная плотность р, кг/м3	Плотность у0, кг/м3	Истинная пористость П(|, %
Кварц	2 650	—	—
Г ранит	2 700… 2 800	2 600… 2 700	0,5… 1,0
Бетон (тяжелый)	2 600… 2 700	2 200… 2 500	8…12
Кирпич керамический	2 500… 2 600	1 400… 1 800	25…45
Древесина	1 500… 1 550	400… 800	45…70
Пенополистирол	1 100… 1 200	15…80	92…99
Сталь	7 800	—	—

Объем образца в естественном состоянии равен сумме объема пор Кпор и абсолютного объема Кабс (объема плотной части мате­риала):

V = V +

г ест г пор ~ г абс*

Абсолютная плотность р — это масса единицы объема матери­ала в абсолютно плотном состоянии:

Р = т/ Кбс-

Насыпная плотность ун — это масса единицы объема, занимае­мого дисперсным материалом в рыхло или плотно насыпанном состоянии:

ун = (m-m{)/V,

где т — масса мерного сосуда с рыхлым материалом; т, — масса пустого сосуда; V — объем сосуда.

Для получения сопоставимых значений ун в рыхлом состоянии мерный сосуд заполняют гипсом с помощью стандартной наклон­ной плоскости, а портландцементом — с помощью стандартной воронки.

Истинная пористость П0 (%) — это степень заполнения объе­ма материала порами:

П0 = (Кпор/ Кест)100 = [(Ксст — Fa6c) / Кест]100 = [(р — Уо)/р]ЮО.

Пористость материалов колеблется в широких пределах (табл.

2.1).

Водопоглощение — это способность материала впитывать и удер­живать в себе воду. Водопоглощение определяют:

по массе —

вм = {ттс — пі)/ m] 100;

по объему —

Во — [(^нас — Wl) / Рп Кесх] 100,

где тнж — масса материала в насыщенном водой состоянии; рв — плотность воды, равная 1 кг/м3.

Капиллярная пористость Пк (%) — это степень заполнения объе­ма капиллярными (открытыми) порами:

Пк = (Ккап/ КСС|)100,

где VKan — объем капиллярных пор.

Эти поры заполняются водой, поэтому VKan приблизительно равен объему воды в порах: VKan = (тнж-т)/р; капиллярная пори­стость равна водопоглощению по объему: Пк = В0. Поэтому вели­чину В0 называют кажущейся пористостью.

Замкнутая пористость П3 (%) — это степень заполнения объема замкнутыми (закрытыми) порами, в которые вода не проникает. Замкнутую пористость можно приближенно определить по разно­сти между истинной и капиллярной пористостями: П3 = П0 — В0.

Все перечисленные ранее характеристики вычисляются по эк­спериментально полученным значениям четырех величин: массы образца в высушенном (т) и водонасыщенном (тнас) состоянии; объема высушенного образца в естественном состоянии (1/,ст) и абсолютного объема (Кабс).

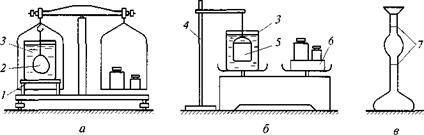
Определение массы производится взвешиванием образцов на аналитических или технических весах.

Высушивание образцов производят в лабораторном сушильном шкафу при температуре (100… 110)°С. Периодически взвешивая образцы, следят за изменением их массы в процессе сушки. Когда масса перестает изменяться, сушку заканчивают и образцы поме­щают в эксикатор (стеклянный сосуд с герметично притертой крышкой) для охлаждения.

Насыщение образцов водой производят, погружая образцы в воду на подкладки, или при постепенном повышении уровня воды в сосуде. Окончание процесса заполнения водой открытых пор определяют по постоянству массы образца при периодическом взвешивании. Перед каждым взвешиванием образец обтирают мяг­кой тканью.

Определение объема образца в естественном состоянии выпол­няется различными методами в зависимости от формы образцов.

Образцы правильной формы (кубы, цилиндры) обме­ряют штангенциркулем и вычисляют объем: Ккуб = abh, где а, b, h — соответственно длина, ширина и высота куба; КЦШ1 = nr2h, где г, h — соответственно радиус и высота цилиндра.

Рис. 2.1. Схемы гидростатического взвешивания (а — образца неправиль­ной формы; б — сыпучего материала) и колба Ле-Шателье (в):

I — подставка; 2 — образец; 3 — сосуд с водой; 4 — штатив; 5 — ведерко; 6 —
уравновешивающий груз; 7 — риски

Образцы неправильной формы подвергают обычному и гидростатическому взвешиваниям в водонасыщенном состоянии и вычисляют объем как разность результатов этих взвешиваний, поделенную на плотность воды.

При гидростатическом взвешивании образец неправильной фор­мы подвешивают к весам с помощью тонкой проволоки, погружа­ют в воду (рис. 2.1, а) и определяют его вес в воде (7ГС = mrcg, который меньше, чем вес в воздухе (70 = mag, на значение вытал­кивающей (архимедовой) силы, равной весу вытесненной воды; GB — Кврвg, где т1С, т0 — масса насыщенного водой образца соот­ветственно при гидростатическом и обычном взвешивании; VB — объем вытесненной воды, равный объему образца (VB= Кест); рв — плотность воды, равная 1 000 кг/м3; g — ускорение свободного падения. Следовательно, Vt„= {т0-тТС)/рв.

Образцы сыпучих материалов (гравия, щебня) испы­тывают также путем гидростатического взвешивания, однако схе­му испытания несколько видоизменяют (рис. 2.1, б). На чашу ве­сов устанавливают сосуд с водой, в который погружают пустое ведерко, подвешенное на тонкой проволоке к штативу. Весы уравновешивают грузом на другой чаше. В ведерко всыпают пор­цию насыщенного водой гравия (щебня). При этом равновесие весов нарушается из-за того, что на гравий действует выталкива­ющая сила. Значение массы Ат, необходимой для восстановления равновесия, поделенное на плотность воды, равно объему зерен гравия: Кест = А/я/р„.

Определить абсолютный объем можно только, превратив об­разец в тонкий порошок. При измельчении открываются закры­тые поры, в которые вода не проникла бы при испытании образ­ца целиком. Чем тоньше измельчен образец, тем точнее будет оп­ределен абсолютный объем.

Объем порошка проще всего отмерить с помощью стеклянной колбы Ле-Шателье, на горле которой между двумя рисками име­ется расширение (рис. 2.1, в). В этот объемомер заливают жидкость до нижней черты, после чего всыпают измельченный в порошок материал, пока жидкость не поднимется до верхней черты. Объем всыпанного материала равен объему между рисками (обычно 20 или 10 см3).

2.1. Общие сведения

В соответствии с агрегатным состоянием дисперсионной среды (см. подразд. 1.1) свойства материалов можно подразделить на три группы.

1. Технические свойства материала как готового продукта, ко­торые можно, в свою очередь, подразделить на общие свойства, характерные для всех материалов, и специальные. К общим отно­сятся физико-механические свойства, долговечность; к специаль­ным свойствам относятся теплопроводность, паро — и водонепро­ницаемость, стойкость к истиранию, звукопоглощение и другие свойства, определяющие назначение материала.

2. Технологические свойства, характеризующие способность исходных материалов при получении изделий перемешиваться, экструдироваться, формоваться, уплотняться. К технологическим свойствам относятся пластичность, вязкость, предел текучести, удобоукладываемость, способность к той или иной обработке, скорость твердения и т. д.

3. Свойства сырьевых компонентов, предопределяющие каче­ство конечного продукта. Например, для бетона важны свойства цемента, заполнителей и добавок. Качество керамического череп­ка зависит от свойств глины, а пластмасс — от свойств полиме­ров и наполнителей.

Экспериментально получаемые характеристики материалов за­висят от методики их определения. Поэтому технические требова­ния к материалам формулируют исходя из стандартных методов испытаний.

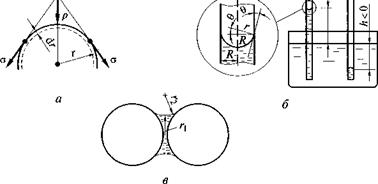
Явления смачивания. Если молекулы жидкости взаимодейству­ют с молекулами твердого тела сильнее, чем между собой, то капля жидкости растекается по поверхности — смачивает ее. При этом краевой угол смачивания 0 < 90°, a cos 0 > 0 (рис. 1.2, а).

Если между собой молекулы жидкости взаимодействуют силь­нее, чем с молекулами твердого тела, то капля жидкости не рас­текается: 0 > 90°, cos 0 < 0. Крайними случаями этого процесса являются полное смачивание, когда 0 = 0, cos 0 = 1 (жидкость растекается до образования мономолекулярного слоя) и полное несмачивание, когда 0 = 180°, cos 0 =-1 (капля стремится сохра­нить сферическую форму).

Способность поверхностей тел смачиваться водой является ре­зультатом действия трех сил поверхностного натяжения о на гра­ницах твердое тело —газ (т — г); твердое тело—жидкость (т—ж);

а

жидкость —газ (ж—г) (рис. 1.2, б). Растекание капли прекратит­ся, когда наступит равновесие этих сил, действующих на каждой единице длины периметра смачивания. Условие равновесия выра­жается уравнением Юнга:

ат_г = ат_ж + ox_rcos 0 или cos 0 = (ат_г-ах_ж)/стж_г. (1.1)

По способности смачиваться водой поверхности тел подразде­ляются на гидрофильные (смачиваемые) с cos 0 > 0 и гидрофобные (несмачиваемые) с cos 0 < 0.

Краевой угол смачивания составляет: для кварца — 0°, малахи­та — 17°, графита — 55°, талька — 69°, парафина — 106°, тефлона —

Реальная поверхность никогда не бывает совершенно чистой. Присутствие на поверхности загрязняющих веществ, оксидных пленок, адсорбированного воздуха оказывает сильное влияние на смачиваемость. Гидрофильная поверхность кварца, покрытая тон­кой пленкой масла или жира, становится гидрофобной.

Адгезия и когезия. В гетерогенных системах различают межмоле­кулярные взаимодействия (притяжение молекул) между разными фазами (адгезия) и внутри одной фазы {когезия).

Силы адгезии действуют на очень малых расстояниях. Для их возникновения необходим контакт фаз. В случае твердых тел обес­печить значительную площадь контакта чрезвычайно трудно даже при высоком давлении. Если сложить пластины с плоскими шли­фованными поверхностями, то можно почувствовать их слипание. Значительные силы адгезии возникают, если смочить поверхнос­ти пластин водой или другой жидкостью, так как жидкость всту­пает в контакт с твердым телом по всей площади смоченной по­верхности. Таким образом, чтобы обеспечить хорошее прилипа­ние, необходимо одну из фаз перевести в жидкое или вязкоплас­тичное состояние. Этот принцип используется при склеивании, пайке, сварке материалов, нанесении на поверхность лакокра­сочных, гидроизоляционных покрытий, штукатурных растворов, получении композиционных материалов (пластмасс, бетона, ке­рамических изделий), когда наполнители или заполнители сме­

шивают с жидким связующим, которое впоследствии переводят в твердое состояние.

Когезионное взаимодействие характеризуют работой когезии 1VK, Дж/м2, необходимой для разрыва фазы, по сечению единич­ной площади. При разрыве фазы образуются две поверхности (пло­щадь каждой равна единице) с поверхностным натяжением в слу­чае жидкости <тж_г, а в случае твердого тела ох__г (рис. 1.3, а). Сле­довательно, работа когезии жидкости равна WK = 2ож_г, а твердо­го тела — = 2от_г.

Работа адгезии определяется энергией, затраченной на разрыв связи по контакту между фазами, отнесенной к единице площади. Определим работу адгезии Wa, Дж/м2, между жидкостью и твер­дым телом в газообразной среде. До разрыва поверхностная энер­гия единицы площади контакта равна от_ж. После разрыва образу­ются две поверхности с поверхностным натяжением, равным на одной из них аж_г, на другой — от_, (рис. 1.3, б). В этом случае работа адгезии определяется по уравнению Дюпре:

В/, — ож_г + от_г— от_ж. (1.2)

Выразим от_г из уравнения (1.1) и подставим в уравнение (1.2). Получим: fVa = стж_г(1 + cos0). Величины аж_г и cos в определяют­ся экспериментально.

Отношение работ адгезии и когезии для случая твердое тело — жидкость зависит только от краевого угла смачивания:

К/ И4 = стж-і( 1 + СО50)/2ОЖ„Г = (1 + cos0)/2.

При cos0 = 1 (полное смачивание) Wa = WK, т. е. разрыв при растяжении равновероятен как по контакту, так и по жидкости. При cos0 =-1 (полное несмачивание) Wa = 0, следовательно, нет адгезии. В промежуточном случае, при cos0 = 0, Wa = 0,5 WK.

		Жидкость				Жидкость
Жидкость	/			Жидкость	/
а = 0		сг Газ -Г	ж — Г	<*т-ж		ч стж Газ -г
£=1			5=1	G’p
——		Жидкость		Твердое тело		Твердое тело

а

б

Рис. 1.3. Иллюстрация к выводу уравнения Дюпре: а — когезия; б — адгезия; S — площадь столбика

о л -s; Рис. 1.4. Происхождение внутреннего давления в жидкости (а), поднятие (опускание) жидкости в капилляре (б) и удержание твердых частиц вод­ной манжетой (в)

Работу адгезии между твердыми фазами определить невозмож­но, так как обычно неизвестно поверхностное натяжение на гра­нице твердое тело — воздух. В этом случае адгезию характеризуют силой, необходимой для разрыва адгезионного соединения по еди­нице площади.

Капиллярные явления. Благодаря поверхностному натяжению жидкости стремятся принять сферическую форму. Этому препят­ствует сила тяжести, которая при большом объеме жидкости де­лает поверхность плоской. С уменьшением объема жидкости Ксила тяжести снижается пропорционально кубу радиуса капли, в то время как поверхность капли уменьшается пропорционально квад­рату радиуса.

При малых размерах частиц силы поверхностного натяжения начинают преобладать над силами тяжести и поверхность приоб­ретает кривизну, благодаря которой капля оказывается сжатой внутренним давлением р, обусловленным силами поверхностного натяжения о и направленным к центру кривизны (рис. 1.4, а). Под действием этого давления объем капли уменьшается на 8Ки со­вершается работа рЪ V В то же время сокращается площадь поверх­ности капли на 5.S’ и уменьшается ее поверхностная энергия на o8S.

При равновесии, если считать температуру тела неизменной, согласно закону сохранения энергии можно записать (уравнение Лапласа):

рЪУ — a&S, или р = об^/бК. (1.3)

Для сферы

где г — радиус сферы.

Тогда р = 2а/г, где 1 /г — это дисперсность. Чем больше дис­персность, тем выше внутреннее давление в капле.

Искривление поверхности жидкости (образование мениска) имеет место в узких капиллярах. В зависимости от направления кривизны мениска (направления внутреннего давления р) проис­ходит поднятие или опускание жидкости в капилляре (рис. 1.4, б). Это определяется смачиваемостью стенок капилляра. В гидрофиль­ном капилляре (0 < 90°) мениск вогнутый, происходит поднятие жидкости; в гидрофобном капилляре (0 > 90°) мениск выпуклый, жидкость выталкивается из капилляра.

Рассчитаем высоту h поднятия жидкости в гидрофильном ка­пилляре радиусом R. В состоянии равновесия капиллярное давле­ние р, определяемое по формуле (1.3), уравновешено весом стол­бика жидкости, равным рgh, т. е. рgh = 055/8К Полагая, что мениск имеет сферическую форму (65/5V = 2/г), и учитывая соотношение между радиусом мениска г и радиусом капилляра R (г = R/cos0), получаем

где о — поверхностное натяжение воды; 0 — краевой угол смачи­вания; р — плотность воды; g — ускорение свободного падения.

Из формулы (1.4) следует, что для одной и той же жидкости (о = const, р = const) высота капиллярного поднятия тем больше, чем меньше радиус капилляра и выше его гидрофильность (cos0). При cos 0 < 0 (гидрофобный капилляр), h < 0 жидкость не втя­гивается в капилляр. Для того чтобы вдавить жидкость в гидро­фобный капилляр до уровня h = 0, нужно приложить давление р =-2ocos0/7?. На этом принципе основан способ гидроизоляци­онной защиты конструкций. Материалы обрабатывают специаль­ными проникающими составами, которые покрывают стенки ка­пилляров тончайшей гидрофобной пленкой (см. подразд. 14.12). При этом жидкая влага не может проникнуть в поры материала, а пары воды могут свободно выходить из пор.

Бетонная смесь и керамическая масса обладают связностью в основном за счет сил поверхностного натяжения воды, действу­ющих в водных манжетах, имеющих два радиуса кривизны (рис. 1.4, в). Радиус ги лежащий в плоскости, перпендикулярной ри­сунку, всегда больше радиуса г2, лежащего в плоскости рисунка, поэтому давление в водной манжете ниже внешнего, что и спо­собствует удержанию частиц вместе.

Адсорбция. Поверхность раздела фаз, обладая свободной энер­гией, притягивает к себе атомы (ионы) или молекулы веществ,

находящихся в газовой фазе или жидком растворе, что ведет к понижению поверхностной энергии. Это явление называется ад­сорбцией, а обратный процесс называется десорбцией. В результате адсорбции концентрация вещества в объеме раствора снижается, а в поверхностном слое возрастает до тех пор, пока не установит­ся равновесие. Если в растворе находится несколько веществ, то предпочтительнее адсорбируется то, которое сильнее уменьшает поверхностное натяжение. Твердая фаза является адсорбентом (ве­ществом, на поверхности которого происходит адсорбция) по отношению к жидкости или газу. На поверхности раздела жид­кость-жидкость или жидкость —газ могут адсорбироваться мо­лекулы как из одной, так и из другой фазы. В этом случае адсорбат (адсорбированное вещество) представляет собой разделительный слой между ними.

Адсорбция бывает физической — обратимой и химической (или хемосорбцией) — необратимой. При физической адсорб­ции между адсорбентом и адсорбатом действуют силы межмоле­кулярного притяжения, а при химической адсорбции — силы химической связи (силы, которые действуют между атомами в молекулах). При хемосорбции происходит химическая реакция между адсорбентом и адсорбатом с образованием поверхност­ной молекулы, одна часть которой принадлежит адсорбенту, а другая — адсорбату.

Адсорбцию характеризуют величиной

А = Ms/S,

где Ms — масса адсорбата в поверхностном слое; S — площадь межфазной поверхности.

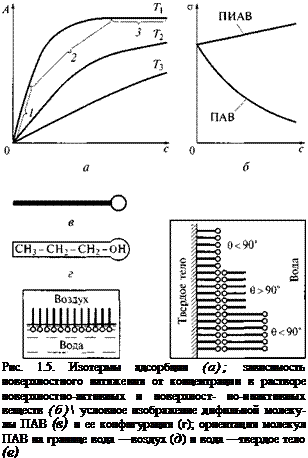
Изотермы адсорбции из раствора (графики зависимости адсорб­ции А от концентрации растворенного вещества с при постоян­ной температуре Т) приведены нарис. 1.5, а(Т3> Т2> Г,). Крутой подъем изотермы (участок 1) характерен для относительно сво­бодной поверхности адсорбента. Полному насыщению поверхнос­ти адсорбатом соответствует участок 3. Участок 2 является проме­жуточным. С повышением температуры усиливается тепловое дви­жение молекул и адсорбция уменьшается, однако предел, к кото­рому она стремится, остается тем же, только для его достижения требуется высокая концентрация, часто нереализуемая.

При адсорбции выделяется теплота, так как снижается поверх­ностная энергия адсорбента.

Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называется поверхностно-активным (ПАВ). Вещества, повышаю­щие поверхностное натяжение раствора с увеличением концент­рации, называются поверхностно-инактивными (ПИАВ) (рис. 1.5, б). Такими веществами по отношению к воде являются неоргани-

д е

ческие соли, которые взаимодействуют с водой сильнее, чем мо­лекулы воды между собой.

Молекулы ПАВ дифильны, т. е. имеют гидрофобную (выталкива­емую из воды) углеводородную часть (цепочку из групп СН2) и гидрофильную (втягиваемую в воду) функциональную группу: —СООН, —NH2, —ОН, —О — , —S020H и др. В условном изоб­ражении дифильной молекулы функциональную группу обозна­чают кружочком, а гидрофобный углеводородный радикал — чер­той (рис. 1.5, в, г). В адсорбционном слое дифильные молекулы обращены полярной группой к полярной фазе (например, к воде), а неполярным углеводородным радикалом — к неполярной фазе (например, к воздуху) (рис. 1.5, д). На твердой поверхности ПАВ способны образовывать полимолекулярные слои (рис. 1.5, ё), при­
чем от числа мономолекулярних слоев зависит, будет ли поверх­ность гидрофильной (0 < 90°) или гидрофобной (0 > 90°).

Широко применяются ПАВ в технологии строительных мате­риалов в качестве добавок пластификаторов бетонной смеси, по­лимерных композиций, керамической массы; эмульгаторов и ста­билизаторов в лакокрасочных материалах; пенообразователей при получении пенобетона и пеносиликата и др.